Dimensionality#

Authors: Jonathan Hargreaves, Amelia Gully

Warning

This part of the site is currently under development. Its content is incomplete.

Will the mesh be set up in one, two or three dimensions? What about axisymmetry? The more dimensions, the greater the computational cost of your model. If your model is regular or symmetrical, you may be able to exploit this to reduce the problem size.

Note

For FEM & FDTD this modifies the PDE. For BEM, this modifies the Green’s function. Compactness can be an issue for the latter.

1D#

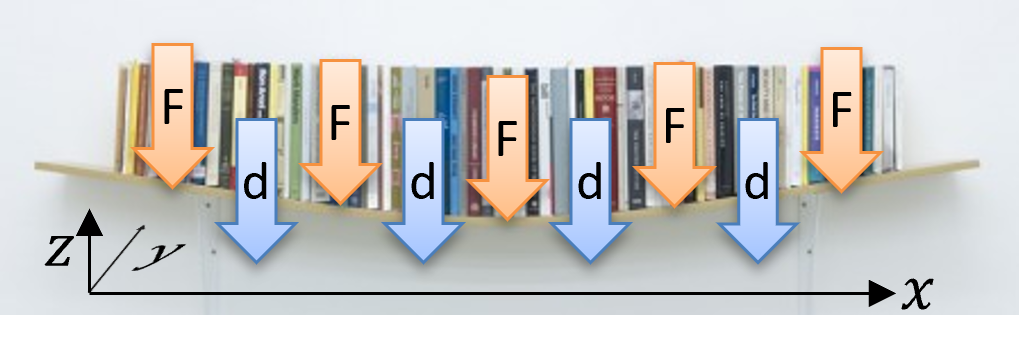
../_images/geom-and-mesh-dimensionality-1D.png

Fig. 8 1D Geometry. Image credit: Jonathan Hargreaves#

Decribe here what the image shows

  • Domain is an interval

  • Boundaries are points

2D#

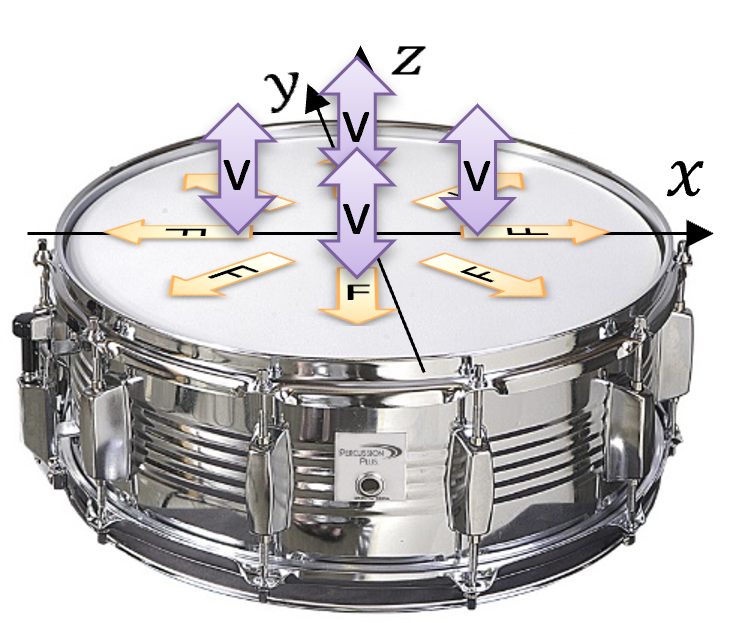
../_images/geom-and-mesh-dimensionality-2D.png

Fig. 9 2D Geometry. Image credit: Jonathan Hargreaves#

Decribe here what the image shows

  • Domain is an area

  • Boundary is a line

3D#

../_images/geom-and-mesh-dimensionality-3D.png

Fig. 10 3D Geometry. Image credit: Jonathan Hargreaves. Depicts the University of Salford Listening Room.#

Decribe here what the image shows

  • Domain is a volume

  • Boundary is a surface

Examples Computational Cost Savings - Meshing a Loudspeaker#

2D Axisymmetric#

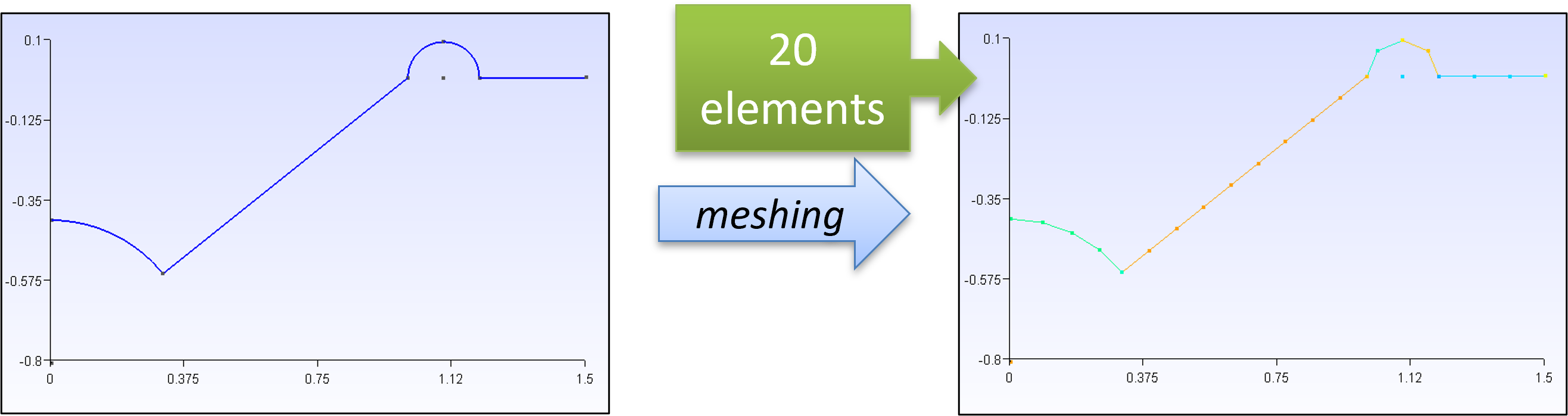
../_images/geom-and-mesh-meshing-axi2D.png

Fig. 11 2D Axisymmetric Mesh. Image credit: Jonathan Hargreaves. Produced using Gmsh 20 elements.#

Full 3D#

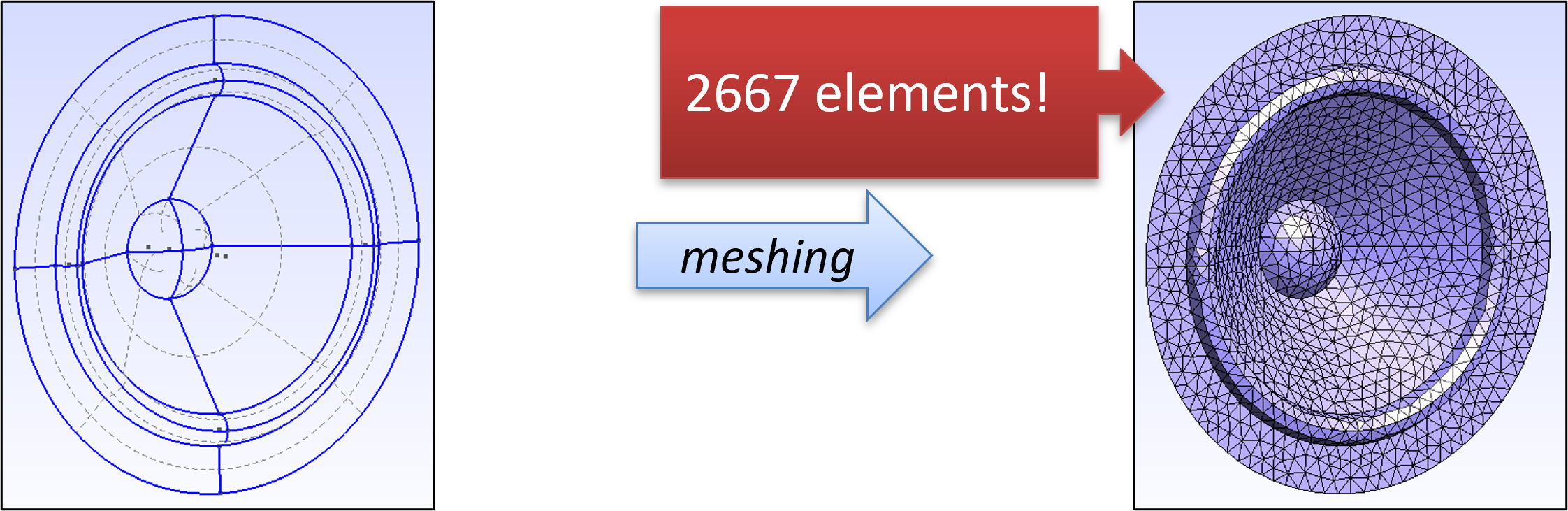
../_images/geom-and-mesh-meshing-3D.png

Fig. 12 3D Mesh. Image credit: Jonathan Hargreaves. Produced using Gmsh 2667 elements.#